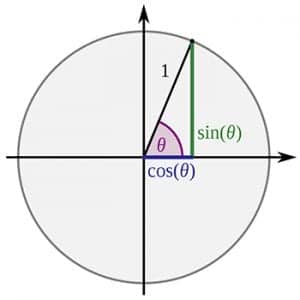
If you’re learning the unit circle, don’t blame yourself if you find it frustrating. It’s pretty intense.
And as you already know, need the unit circle when solving for the:
- Sine
- Cosine
- Tangent of an angle
But let’s not get into a tedious discussion of how the unit circle works. I’m not going to drown you in each and every detail.
Instead, on specific memory goals, like how to remember the radians on the unit circle.
There’s actually a fun and easy way to do this, and so let’s dive in.
How to Memorize the Unit Circle Quickly in 6 Steps
Chances are, many of the techniques you’re about to discover are new to you.
If you approach them with a spirit of experimentation and an open mind, they will help you memorize a lot more than just the unit circle.
This is important because mathematics and geometry is filled with all kinds of complicated equations. You want a technique that helps you conquer this specific learning goal and is adaptable.
That’s why the first suggestion is going to sound a bit counterintuitive.
One: Consider Abandoning the Unit Circle Hand Trick
Now, I’m not the kind of person who says, “don’t even bother trying” something like the Unit Circle Hand Trick.
But I tried it and found it impractical for deliberately memorizing this kind of information. I don’t know about you, but my fingertips are too small for encoding large amounts of digits.
However, there are some cool aspects to the idea, so if you do want to use this technique, spread out your hand.
When you look at your palm, let your pinkie finger represent the positive x axis. Let your thumb represent the positive y axis. This gives you the first quadrant of the unit circle in the palm of your hand (so to speak).
Next:
- Assign 90° to your thumb
- Assign 60° to your pointer finger
- Assign 45° to your middle finger
- Assign 30° to your ring finger
- Assign 0° to your pinkie
That’s pretty easy, but how are you going to remember that 30° is π/6?
That’s coming up.
Two: Learn the Memory Palace Technique
Instead of trying to compress all kinds of information onto a small space like your hand, give yourself more room by using a wall. Here’s what I mean:
If you take your hand and imagine it projected on a wall, now you have a lot more space to work with.
But there’s even a better way to use the Memory Palace technique for memorizing the Unit Circle.
Three: Divide Your Memory Palace Into Five Areas
Take that same wall from a home, classroom, church (or whatever you like) and divide it into five separate areas. Like this:
Do this mentally. Don’t overthink it. The division of space doesn’t have to be perfect. It just needs to be functional.
If you like, you can still use your hand as a reference:
Next, you’ll create some associations so you can remember the different equations.
Four: Use Associations For The Numbers And Equations
This is where the rubber meets the road.
To rapidly create associations of numbers and symbols, you’ll need to create a few simple lists.
For the digits 0-9, learn the Major System. This will let you turn numbers into words. For example, 90 in my system is Baz Lurhmann because 9 can be represented by ‘b’ and 0 can be represented by ‘z.’
Using a highly memorable celebrity makes remembering numbers much easier!
For symbols, figure out the symbols you need to memorize and create associations. For example, a ° could be a donut. Thus, for 90° we can imagine Baz Luhrmann eating a donut.
Five: Place Your Associations In Your Memory Palace
As you can see, it’s a lot easier to mentally place Baz Luhrmann with a donut on your wall than it is on the small space of your thumb.
How exactly you place these images in space is up to you. I like to think about it as “weaving” theme into a room, or hanging from a tree. There are lots of ways to do it, but you’re basically bringing space and association together with the information you want to learn.
When you want to add more, such as π/6, you can integrate a piece of pie and your image for six. You can also add all the degrees and radians, and if you need more space, move to another wall.
To learn more about how all this works in a compact, course format:
Six: Expand To Either The Pegword Method Or A 00-99 PAO
Eventually you’ll want to memorize facts, such as that a 210 degree angle has a radian of 7????/6.
To do this, you’ll want to have a lot of associations come to mind quickly. This is no problem and very useful for anyone involved in any branch of mathematics.
Here’s an example:
7????/6 can have a single image using the pegword method. The 00-99 approach is covered in that resource as well.
To share my mnemonic example, I would have Jack Nicholson throwing a donut at Johnny Cash with a ???? tattoo on his forehead.
For more mnemonic examples, check out this video on memorizing equations:
Seven: Use Recall Rehearsal For Long Term Memory
All of the fun and games you’ve just learned will help you remember with memorizing the Unit Circle. But to get it into long term memory, you’ll want to follow a small set of “repetition rules” using your Memory Palace.
In brief, you need to recall the information in your Memory Palace a few times. And you need to do it in a way that harnesses the power of the primary, recency and serial positioning effect.
To this, use the easy way to memorize the unit circle described above. Then recall the associations and the target information as you travel the Memory Palace:
- Forward
- Backward
- Skip the stations (Thumb, Middle, Pinke, Ring, Pointer)
The last one will feel weird, but it makes sure that you’re giving both primacy and recency effect to each piece of information.
Unit Circle Tricks That Don’t Suck
I’ll never forget when Robert Spraggs posted his university exam scores. He said, the “Magnetic Memory Method Masterclass makes learning not suck.”
True, what you’ve learned today might take a bit of setup. But learning these memory techniques need only take 1-2 afternoons. I’ve seen people pick up the techniques even faster than that.
And once you have them, you can remember anything you want at laser fast speeds.
So what do you say? Does learning the unit circle seem more doable now?
