Would you like to master mental math using the Trachtenberg Method?
If so, you’re in luck.
On this page, you’ll learn what it is and how to use it.
More importantly, you’ll learn how to remember the steps you need to follow in order for the Trachtenberg method of math to work for you.
Ultimately, it’s forgetting how the system works that causes most people to struggle with it.
But we’re going to permanently remove that struggle right now.
So if you’re ready to use one of the most powerful methods of speed calculation, you’re in the right place.
Let’s dive in!
What Is the Trachtenberg Method?
Imagine being held in a Nazi concentration camp.
That’s what happened to Jakow Trachtenberg, engineer and later founder of the Mathematical Institute in Zurich, Switzerland.
Although he was born in Odessa, he eventually moved to Germany. There, he criticized Hitler, who incarcerated him for this “crime.”
While imprisoned, Trachtenberg kept his mind – and his hopes – alive by developing techniques for solving mathematical problems at a rapid pace.
Eventually, he escaped and taught his system of speed calculation to others with great success.
The system itself is a set of mathematical operations. By using these operations, the steps of the Trachtenberg approach allow you to solve arithmetic problems quickly.
How to Learn the Trachtenberg System
To learn the Trachtenberg System, it’s important to understand what it’s for and what it isn’t for.
Generally, it’s for arithmetical multiplications that you want to solve for yourself (for practice or practical outcomes). But it can also be used to check the accuracy of calculations made by others.
Here are the recommended steps so you learn it thoroughly and well.
One: Learn the Vocabulary of the System
Here are the terms Trachtenberg used:
- Multiplicand: the number you want to multiply (i.e. 67324)
- Multiplier: the number you are multiplying by (i.e. 8)
To express this equation using his system, you would have:
67324 x 8
You would write the answer underneath the line:
67324 x 8
538592
There are two more terms to learn;
- Number: the specific digit you’re dealing with during the calculation
- Neighbor: the figure to the right of the number you’re working on
For example, in 67324, 4 has no neighbor because there is no number to its immediate right.
2 is a number and 4 is its neighbor. 3 is a number and 2 is its neighbor, etc.
Two: Learn the Rules For Each Task
The hardest thing about the Trachtenberg System is that there’s more than one rule. You have to know the right rule for completing the specific task you’re working on.
For example, you operate a little bit differently when multiplying by 11 than you do when multiplying by 12. You also operate differently when performing addition.
Let’s start with a simple example first. Then we’ll get into the variations of the rules.
Three: Choose a Number To Add or Multiply
When learning the Trachtenberg system, it’s best to start small.
I suggest starting with a three-digit number at most. And choose just one kind of calculation.
Let’s choose 623 to take one example and multiply it by 11.
Four: Apply the Right Rule
Remembering that a neighbor is always to the right of the number you are working with, here’s our equation:
623 x 11
In this style of equation, we start by drawing down the first number that has no neighbor. That number is 3.
623 x 11
3
Next, we move one number to the left. In this case, that number would be 2. We add this number together with its neighbor, which makes 5. Add that sum to the equation:
623 x 11
53
Next, move to the next number to the left, which is six. Add it to its neighbor, which is 2. You’ll get an 8. Add it to the equation.
623 x 11
853
Finally, draw down the digit furthest to the left. In this case, that’s the 6.
623 x 11
6853
Voila. You now have the correct answer.
Five: Learn the Gotchas!
Warning: There’s an anomaly in this approach that arises depending on the multiplicand.
Let’s say you’re working with 734×11.
When you get to the part where you have to add 7+3, you’ll get a 10. You just need to place the zero in your equation and then carry over the remaining one. Add this remainder to the final number.
The steps will look like:
734x11
4
734x11
74
734x11
074
734x11
8074
You have to do this any time the two digits you’re adding produce an answer greater than 10.
Six: Learn All the Rules for One Kind of Operation
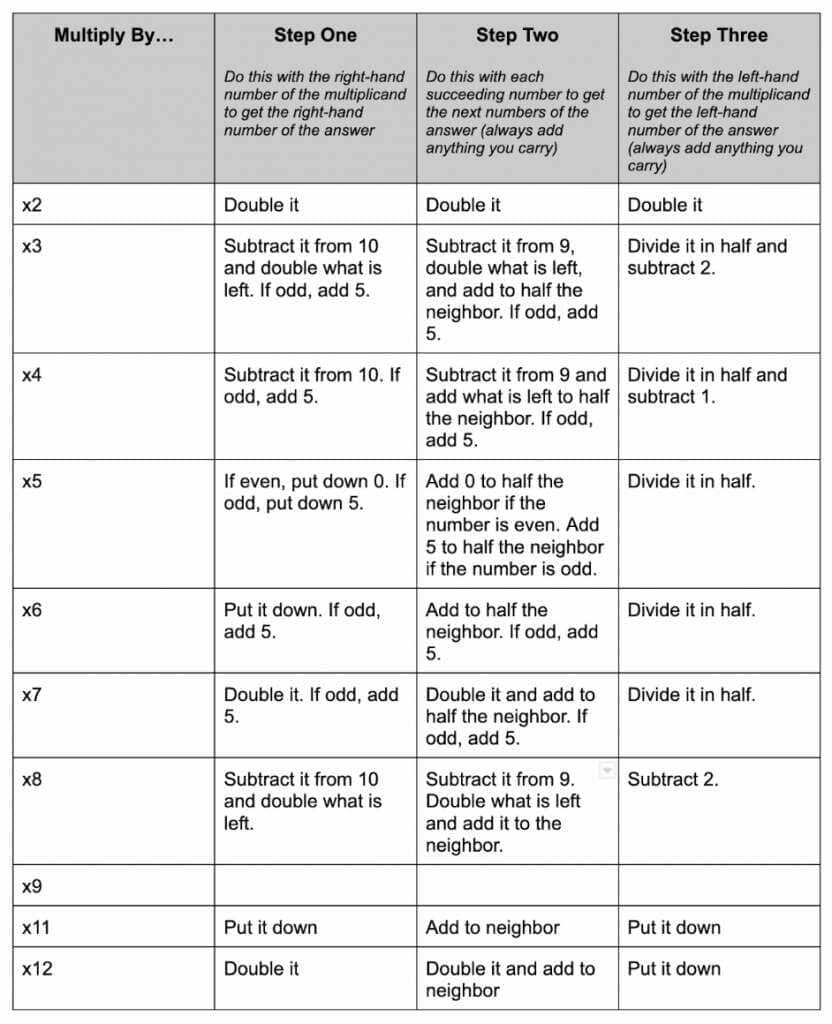
Because there are rules and anomalies along the way when learning the Trachtenberg system for multiplication, I created this table for you:
As you can see, for each multiplication step, there are individual rules. These are in Anne Cutler’s book with Rudolph McShane that teaches you the formulas for division, square roots and more. It’s called The Trachtenberg System of Basic Mathematics.
Seven: Commit the Rules and Anomalies To Memory
At first glance, the formulas that make up the Trachtenberg System seem like a TON to memorize.
Not if you know how to use a Memory Palace.
And not if you’re willing to take it one formula at a time.
All you have to do is take a wall in a Memory Palace. Then recreate one of the formulas in that space by dividing it to accommodate the rule.
In this case, you’ll also want to know the Major System, or have a PAO System. To keep focused, I won’t be teaching them here, but you can learn them both quickly on their respective blog posts.
Here’s a quick visual Memory Palace example for one of the rules we’ve worked with today:
Step One: Since 11 is a toad in my Memory Palace, and the first step is to drop down the first number, I’ll imagine my toad giving the thumbs down.
Step two: Add the next number to its neighbor. To do this, I’ll imagine the toad’s neighbor bringing him some cookies. I’ll place this association in the middle of my Memory Palace wall.
Step Three: But the toad doesn’t like the gift of cookies. So he drops his thumb down as a reminder that the third step in this Trachtenberg formula is to drop down the final number.
How to Use the Trachtenberg Method To Solve Any Equation
The best way to understand how to apply this method is to start working through an example yourself.
Let’s take 210 x 41.
You’ll want to put as many zeros in front of the first multiplier as there are in the second digit. Your equation will now look like this:
00210 x 41.
Write this out on paper, but also think about the math mentally. Here’s how I notated this equation for myself.
The trickiest part is the first step. You need to remember that when linking the first number to the newly fashioned number, it goes “into the void,” so to speak. In the example above, you’ll see that the 4 is linked to a 0.
After that, you progressively move by linking the individual parts of the equation by moving from the right to the left.
This is incredibly fast, and if you check your calculator, you’ll see that the result is correct.
The best part?
Solving math problems this way is a lot of fun.
Again, you’ll want to work on working out problems using the Trachtenberg Method both on paper and in your mind using mental imagery. I suggest practicing with numerous equations over a 90-period. This amount of practice will seriously rewire your brain and make you a much stronger mathematician.
Learn the Trachtenberg Method Fast!
As you can see, these formulas are interesting and fun.
All you need to do is commit them to memory.
And now you have a simple means of doing so based on the example above.
If you’d like to learn more about the Memory Palace techniques, register for my free memory improvement course today:
You’ll discover more about how to add any calculation rapidly into your long term memory.
No matter what mathematical operation you need to know, you can learn to remember it forever.
Enjoy!
Interesting
Thanks for checking it out, Don. It is indeed a neat tool to use.
This is an incredible formula never come across it before but it’s great.
Yes, it’s quite something. Thanks for stopping by.
interested. I really appreciate the simplicity of it
So much math is incredibly simple, isn’t it?
I reached this method through a movie called Gifted (2017) and in real this is very interesting.
Very cool – thanks for mentioning it. I’ll check it out!
When learning to deal roulette about 50 years ago, I was taught to multiply two digit numbers by eleven for one of the payouts. I was told to just add the digits together and place result in between the digits I have used this ever since and just learned it is the Trachtenberg method. Still learning….
Thanks for sharing this fascinating background!
Are there other calculation tricks you picked up from working in this field?